(New tips are continually added to these pages. Check back in a few months' time for more)

TOPIC 12: Alternating Currents and Rectification

Tip 1:

How to find root-mean-square voltage or current? The procedure is to square the waveform first, then find the mean, then finally root the mean.

The r.m.s value of standard waveforms have to be memorised, eg.

Normal Sine/ Cosine Wave: V_rms = V_o/Ö2

Full-Wave Rectified Sine/Cosine Wave: V_rms = V_o/Ö 2

Half-Wave Rectified Sine/Cosine Wave: V_rms = V_o/ 2

Direct Current: V_rms = V_o

Square Wave with Max. at Vo and Min. at -Vo: V_rms = V_o

Pulse Train with Pulse Width W and Period T: V_rms = (Ö(W/T)V_o

For more complex waveforms, there are 2 methods to find the r.m.s.

Method 1 (Integration)

First, square the waveform. Then integrate the squared waveform to find the area under the graph. Next divide the integral by the period to find the mean. Finally, root the mean to get Vrms.

Method 2 (Cut-And-Paste Method or what I call the Ice Cream Method)

Let's use the normal sinusoidal waveform as our example (refer to animations below).

Step 1: Draw the original sinusoidal graph V = V₀ sin wt (the Red one).

Step 2: Square this graph to get V² = V₀² sin² w t (the Green one).

Step 3: Imagine that the green squared graph are scoops of ice cream resting on a tray (the tray is the X axis).

Step 4: Turn on the oven to melt the green ice creams so that they become ice water (the blue line).

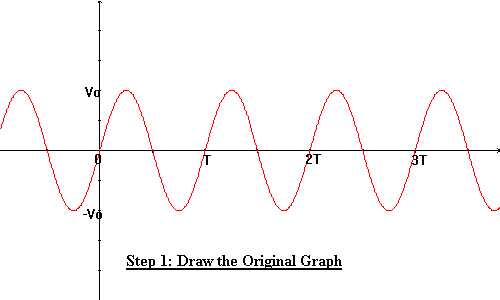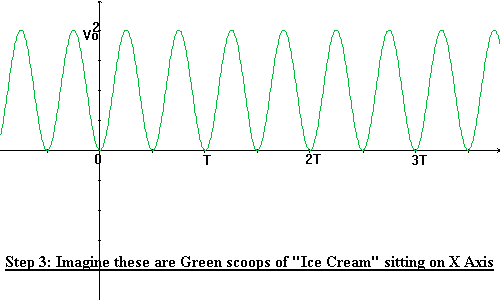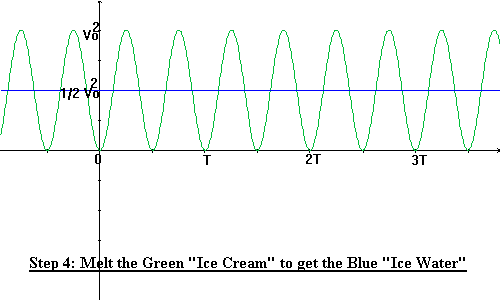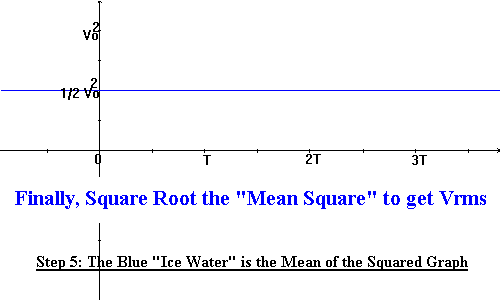
Step 5: The blue line is the mean of the squared graph. In our example, the height of the ice cream is V₀² so half the height (the mean) is V₀²/2.

Finally, root the mean (V₀²/2) to obtain V₀/Ö2 (proven).

You can try with other waveforms, eg. full wave rectified, half wave rectified, triangular, square, or saw-tooth waves.